гнуплот
17 коммент.
Для того, чтобы указать gnuplot строить графики с погрешностями, строка с командой plot в скрипте должна содержать директиву with errorbars:
- погрешности откладываются для данных по оси Х: with xerrorbars
- погрешности откладываются для данных по оси Y: with yerrorbars
- погрешности откладываются для данных по обоим осям: with xyerrorbars
# X Y dX dY
1.0 1.2 0.8 1.5
2.0 1.8 0.3 2.3
3.0 1.6 1.0 2.1
gnuplot> plot "test.dat" using 1:2:3 with yerrorbarsОбщая идея, думаю, понятна: сначала указываются колонки, содержащие данные, а потом колонки, содержащие значения погрешностей. Таблица, любезно утянутая отсюда, даёт прекрасную иллюстрацию:
| Data Format | Column | using | with |
|---|---|---|---|
| (X,Y) data | X Y | 1:2 | lines, points, steps, linespoints, boxes, etc. |
| Y has an error of dY | X Y dY | 1:2:3 | yerrorbars |
| X has an error of dX | X Y dX | 1:2:3 | xerrorbars |
| Y has an error of dY, and X has an error of dX | X Y dX dY | 1:2:3:4 | xyerrorbars |
| Y has a range of [Y1,Y2] | X Y Y1 Y2 | 1:2:3:4 | yerrorbars |
| X has a range of [X1,X2] | X Y X1 X2 | 1:2:3:4 | xerrorbars |
| Y has a range of [Y1,Y2], and X has a range of [X1,X2] | X Y X1 X2 Y1 Y2 | 1:2:3:4:5:6 | xyerrorbars |
Пример 1. Построить график с погрешностями по обеим осям в gnuplot
Итак, есть экспериментальные данные в виде таблицы с разделителями - пробелами:
16 18 0.72 10 whiteLEDS 1 10
12 30 0.61 12 greenUltraBrightLEDS 1 10
8 200 0.45 20 HGlamp 1 15
6 1600 0.35 35 AlGaAsLser 1 50
4 17000 0.28 68 NdYAG-laser 1 900
4 25000 0.27 70 HeNeLaser 1 1100
Нужно построить зависимость первой колонки от второй, при этом погрешности по оси X составляют 7% от данных, а по оси Y указаны в колонке 7. Вот такой при этом получается код для gnuplot:
set terminal postscript 'NimbusSanL-Regu' eps enhanced
set output "./plot/PSFoutofLambdaDeltaLambdavsfromNumberOfElementsPSF.ps"
set encoding koi8r
set xlabel "Light's monochromaticity, {/Symbol l}/{/Symbol D}{/Symbol l}" font "NimbusSanL-Regu,18"
set nokey
set bmargin 4
set ylabel "Number of resolvable points of the PSF's kinoform" font "NimbusSanL-Regu,18"
set logscale x
set grid
set xrange [1:100000]
set mxtics 10
set style line 1 lt 1 pt 7 ps 0.5
plot "./PSFoutofLambdaDeltaLambda.txt" using 2:((300/$1)**2):7:(((300/$1)**2)*0.07) with xyerrorbars linestyle 1, "./PSFoutofLambdaDeltaLambda.txt" using 2:((300/$1)**2) smooth bezier with lines
Результат строительства графика:
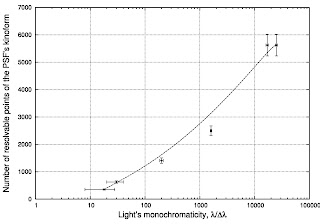 Что в этом коде (и графике) есть примечательного, заставившего меня таки покопаться в мануале?
Что в этом коде (и графике) есть примечательного, заставившего меня таки покопаться в мануале?Ну например то, что при строительстве данных с погрешностями вам не удастся использовать линии: опция with linespoints не пройдёт и gnuplot будет выдавать ошибки. И это правильно: экспериментальные данные соединять непрерывной линией - моветон. Так что используем только linestyle 1 который определён так: set style line 1 lt 1 pt 7 ps 0.5 Это значит: тип линии 1, стиль точек 7, размер точки на графике 0.5. Крайние точки я просто соединил кривой Безье, о чём честно написал в коде графика: smooth bezier with lines
Ну и наконец нужно было построить квадратичную зависимость по оси Y, что реализовано так: ((300/$1)**2) то есть число 300 делится для каждой точки на значение в первой колонке, результат возводится в квадрат.
Пример 2. Построить график с погрешностями и аппроксимацией в gnuplot
Задачка посложнее: здесь требовалось экспериментальные точки аппроксимировать прямой линией и погрешностями. Из части данных нужно вычесть постоянную составляющую, так что работы для gnuplot хватает. Итак, сеанс чёрной магии с полным её разоблачением:
#! /usr/bin/gnuplot -persist
set terminal postscript 'NimbusSanL-Regu' eps enhanced solid
set yrange [0.1:10000]
set logscale x
set logscale y
set mxtics 10
set mytics 10
set grid xtics ytics mxtics mytics
set format y "10^{%L}"
set format x "10^{%L}"
set mxtics 10
set output "./plots/1RAWMEANtoSaturateLineApproxcomparingLogscale.ps"
set encoding koi8r
set xlabel "Exposure value, rel. units" font "NimbusSanL-Regu,18"
set ylabel "Signal mean value, DN" font "NimbusSanL-Regu,18"
set key bottom right
set bmargin 4
set style line 1 lt 2 pt 7 ps 1
f(x) = (a*x)+b
fit f(x) "./RAWMEANmeasurementresult" using 4:($3-255.22579) every ::4::35 via a,b
plot "./RAWMEANmeasurementresult" using 4:($3-255.22579):7 title "Digital values of photosensor signal" with yerrorbars linestyle 1, f(x) title "linear fitting function" with line
Сейчас
использовать только точки с 4 по 35-ю every ::4::35 и, наконец, подогнать коэффициенты a и b под данные via a,b.
Здесь я отмечу то, что сам часто забываю: директиву every можно использовать не только при подгонке, но и для других графиков. Для этого полезно иметь перед глазами таблицу, которую изваял автор not so Frequently Asked Questions:
| every I:J:K:L:M:N |
| ||||||||||||
| every 2 | plot every 2 line | ||||||||||||
| every ::3 | plot from the 3-rd lines | ||||||||||||
| every ::3::5 | plot from the 3-rd to 5-th lines | ||||||||||||
| every ::0::0 | plot the first line only | ||||||||||||
| every 2::::6 | plot the 1,3,5,7-th lines | ||||||||||||
| every :2 | plot every 2 data block | ||||||||||||
| every :::5::8 | plot from 5-th to 8-th data blocks |
Теперь осталось построить два графика на одном:
plot "./RAWMEANmeasurementresult" using 4:($3-255.22579):7 title "Digital values of photosensor signal" with yerrorbars linestyle 1, f(x) title "linear fitting function" with line
То есть строим зависимость колонки 3 от 4 и используем колонку 7 как источник погрешности. При этом накладываем аппроксимационную линию с помощью директивы f(x) title "linear fitting function" with line
Собственно, вот итог моих фокусов:
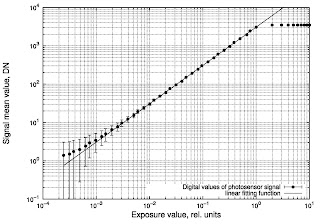
Красиво и вполне себе презентабельно, хоть в Nature отправляй.



