Собственно, наиболее часто в экспериментальной физике требуется строить графики, которые отражают точность измерений - на графиках требуется откладывать погрешности. Так как чаще всего данные организованы в таблицы, построить график с погрешностями в gnuplot нетрудно, однако в этом деле есть ряд подводных камней, о чём ниже.
Для того, чтобы указать gnuplot строить графики с погрешностями, строка с командой plot в скрипте должна содержать директиву with errorbars:
- погрешности откладываются для данных по оси Х: with xerrorbars
- погрешности откладываются для данных по оси Y: with yerrorbars
- погрешности откладываются для данных по обоим осям: with xyerrorbars
Величину погрешности можно посчитать для каждой точки (в зависимости от эксперимента, например, при измерениях на разных пределах) и сделать для этого в файле данных test.dat данных отдельную колонку:
# X Y dX dY
1.0 1.2 0.8 1.5
2.0 1.8 0.3 2.3
3.0 1.6 1.0 2.1
В этом случае, чтобы построить график с погрешностями по оси Y, например, последняя команда в скрипте для графика будет выглядеть так:
gnuplot> plot "test.dat" using 1:2:3 with yerrorbars
Общая идея, думаю, понятна: сначала указываются колонки, содержащие данные, а потом колонки, содержащие значения погрешностей. Таблица, любезно утянутая отсюда, даёт прекрасную иллюстрацию:
| Data Format | Column | using | with |
|---|
| (X,Y) data | X Y | 1:2 | lines, points, steps,
linespoints, boxes, etc. |
| Y has an error of dY | X Y dY | 1:2:3 | yerrorbars |
| X has an error of dX | X Y dX | 1:2:3 | xerrorbars |
Y has an error of dY, and
X has an error of dX | X Y dX dY | 1:2:3:4 | xyerrorbars |
| Y has a range of [Y1,Y2] | X Y Y1 Y2 | 1:2:3:4 | yerrorbars |
| X has a range of [X1,X2] | X Y X1 X2 | 1:2:3:4 | xerrorbars |
Y has a range of [Y1,Y2], and
X has a range of [X1,X2] | X Y X1 X2 Y1 Y2 | 1:2:3:4:5:6 | xyerrorbars |
Для иллюстрации разберу два рабочих примера с построением графиков с погрешностями и аппроксимацией данных.
Пример 1. Построить график с погрешностями по обеим осям в gnuplot
Итак, есть экспериментальные данные в виде таблицы с разделителями - пробелами:
16 18 0.72 10 whiteLEDS 1 10
12 30 0.61 12 greenUltraBrightLEDS 1 10
8 200 0.45 20 HGlamp 1 15
6 1600 0.35 35 AlGaAsLser 1 50
4 17000 0.28 68 NdYAG-laser 1 900
4 25000 0.27 70 HeNeLaser 1 1100
Нужно построить зависимость первой колонки от второй, при этом погрешности по оси X составляют 7% от данных, а по оси Y указаны в колонке 7. Вот такой при этом получается код для gnuplot:
#! /usr/bin/gnuplot -persist
set terminal postscript 'NimbusSanL-Regu' eps enhanced
set output "./plot/PSFoutofLambdaDeltaLambdavsfromNumberOfElementsPSF.ps"
set encoding koi8r
set xlabel "Light's monochromaticity, {/Symbol l}/{/Symbol D}{/Symbol l}" font "NimbusSanL-Regu,18"
set nokey
set bmargin 4
set ylabel "Number of resolvable points of the PSF's kinoform" font "NimbusSanL-Regu,18"
set logscale x
set grid
set xrange [1:100000]
set mxtics 10
set style line 1 lt 1 pt 7 ps 0.5
plot "./PSFoutofLambdaDeltaLambda.txt" using 2:((300/$1)**2):7:(((300/$1)**2)*0.07) with xyerrorbars linestyle 1, "./PSFoutofLambdaDeltaLambda.txt" using 2:((300/$1)**2) smooth bezier with lines
Результат строительства графика:
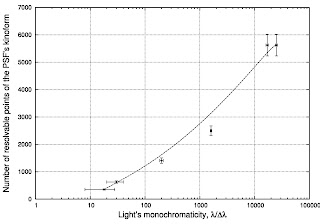 Что в этом коде (и графике) есть примечательного, заставившего меня таки покопаться в мануале?
Что в этом коде (и графике) есть примечательного, заставившего меня таки покопаться в мануале?
Ну например то, что при строительстве данных с погрешностями вам не удастся использовать линии: опция with linespoints не пройдёт и gnuplot будет выдавать ошибки. И это правильно: экспериментальные данные соединять непрерывной линией - моветон. Так что используем только linestyle 1 который определён так: set style line 1 lt 1 pt 7 ps 0.5 Это значит: тип линии 1, стиль точек 7, размер точки на графике 0.5. Крайние точки я просто соединил кривой Безье, о чём честно написал в коде графика: smooth bezier with lines
Ну и наконец нужно было построить квадратичную зависимость по оси Y, что реализовано так: ((300/$1)**2) то есть число 300 делится для каждой точки на значение в первой колонке, результат возводится в квадрат.
Пример 2. Построить график с погрешностями и аппроксимацией в gnuplot
Задачка посложнее: здесь требовалось экспериментальные точки аппроксимировать прямой линией и погрешностями. Из части данных нужно вычесть постоянную составляющую, так что работы для gnuplot хватает. Итак, сеанс чёрной магии с полным её разоблачением:
#! /usr/bin/gnuplot -persist
set terminal postscript 'NimbusSanL-Regu' eps enhanced solid
set yrange [0.1:10000]
set logscale x
set logscale y
set mxtics 10
set mytics 10
set grid xtics ytics mxtics mytics
set format y "10^{%L}"
set format x "10^{%L}"
set mxtics 10
set output "./plots/1RAWMEANtoSaturateLineApproxcomparingLogscale.ps"
set encoding koi8r
set xlabel "Exposure value, rel. units" font "NimbusSanL-Regu,18"
set ylabel "Signal mean value, DN" font "NimbusSanL-Regu,18"
set key bottom right
set bmargin 4
set style line 1 lt 2 pt 7 ps 1
f(x) = (a*x)+b
fit f(x) "./RAWMEANmeasurementresult" using 4:($3-255.22579) every ::4::35 via a,b
plot "./RAWMEANmeasurementresult" using 4:($3-255.22579):7 title "Digital values of photosensor signal" with yerrorbars linestyle 1, f(x) title "linear fitting function" with line
Сейчас маэстро Воланд скромный автор сих строк разоблачит этот опыт. Первое, что надо разоблачить - аппроксимацию прямой. Здесь сначала задаётся функция f(x) = (a*x)+b которая далее подгоняется под данные using 4:($3-255.22579) из которых вычитается постоянная величина (эксперимент такой был). Далее при подгонке я потребовал от gnuplot
использовать только точки с 4 по 35-ю every ::4::35 и, наконец, подогнать коэффициенты a и b под данные via a,b.
Здесь я отмечу то, что сам часто забываю: директиву every можно использовать не только при подгонке, но и для других графиков. Для этого полезно иметь перед глазами таблицу, которую изваял автор not so Frequently Asked Questions:
| every I:J:K:L:M:N | | I | Line increment | | J | Data block increment | | K | The first line | | L | The first data block | | M | The last line | | N | The last data block | |
| every 2 | plot every 2 line |
| every ::3 | plot from the 3-rd lines |
| every ::3::5 | plot from the 3-rd to 5-th lines |
| every ::0::0 | plot the first line only |
| every 2::::6 | plot the 1,3,5,7-th lines |
| every :2 | plot every 2 data block |
| every :::5::8 | plot from 5-th to 8-th data blocks |
Теперь осталось построить два графика на одном:
plot "./RAWMEANmeasurementresult" using 4:($3-255.22579):7 title "Digital values of photosensor signal" with yerrorbars linestyle 1, f(x) title "linear fitting function" with line
То есть строим зависимость колонки 3 от 4 и используем колонку 7 как источник погрешности. При этом накладываем аппроксимационную линию с помощью директивы f(x) title "linear fitting function" with line
Собственно, вот итог моих фокусов:
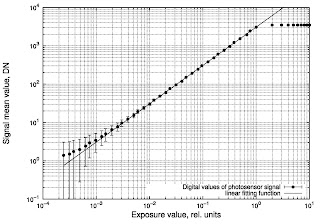
Красиво и вполне себе презентабельно, хоть в Nature отправляй.
 Что в этом коде (и графике) есть примечательного, заставившего меня таки покопаться в мануале?
Что в этом коде (и графике) есть примечательного, заставившего меня таки покопаться в мануале?
17 комментариев: |высказаться!| RSS-лента дискуссии.|
По теме, пожалуй, сказать мне нечего — сам я с такой задачей не сталкивался, да и из применяемых в статье высоких понятий пока что слышал только об апроксимации :) Тем не менее, свой традиционный хит-парад предоставлю:
построить график с
погрешностями
У тебя здесь почему-то br стоит.
указать gnuplot строить графики с погрешностями на двухмерных графиках
Тавтология. Не знаю, как исправить, чтобы было красиво :(
файле test.dat данных
«Файле данных test.dat» звучало бы лучше.
разделителями - пробелами
Тут лучше не тире, а дефис ставить.
Так что только linestyle 1 который определён так: set style line 1 lt 1 pt 7 ps 0.5
Оно-то понятно, что ты имеешь в виду, но как-то нелитературно: это предложение нужно не читать, а слушать — только тогда его можно будет понять с первого раза. Советую переписать.
Так же мне было откровенно лень
Так же из части данных нужно вычесть
Знаешь, у меня появилась мысль: ты мог бы использовать эти свои «так же» в качестве доказательства (поисковым системам или кому там ещё), что автор поста — ты ;)
число 300 делится для каждой точки на значение в первой колонке и результат возводится в квадрат
«И» можно было бы заменить на «а» (и не забыть про запятую перед ним) — мне кажется, тогда читать будет проще.
скромный автор этих строк разоблачит этот опыт
Тавтология. Используй что-то вроде «сей»: «скромный автор сих строк разоблачит этот опыт» или «скромный автор этих строк разоблачит сей опыт».
директиву every можно
Ты код вроде везде зелёным выделяешь, а every здесь не выделил. Это намеренно или просто забыл?
P.S. Написал статью, о которой ты просил ;)
Ну, я тогда тоже сделаю комментарий в предыдущем стиле :) "не трудно" в первом абзаце пишется слитно.
Ещё мне кажется, что наиболее часто в экспериментальной физике для подобных вещей используют ROOT, а гнуплотом удобнее рисовать аналитические функции.
@Programmaster
скромный автор этих строк разоблачит этот опыт
Тавтология. Используй что-то вроде «сей»: «скромный автор сих строк разоблачит этот опыт» или «скромный автор этих строк разоблачит сей опыт».
Это ирония была. Ну и фиг с ней :-)
Остальное исправил. Александр, огромное тебе спасибо!
@lizardie
Ну, я тогда тоже сделаю комментарий в предыдущем стиле :) "не трудно" в первом абзаце пишется слитно.
Исправлено.
Ещё мне кажется, что наиболее часто в экспериментальной физике для подобных вещей используют ROOT
Это вам так только кажется. :-) Из всей кафедры я один слышал про R, но не использовал, а обычно используется Excel. Это без комментариев.
а гнуплотом удобнее рисовать аналитические функции.
Гнуплоту в общем наплевать, что строить, но создавался он точно не для того, чтобы школьные графики делать. На самом деле в хороших домах Европы его весьма жалуют и используют.
Спасибо уважаемым комментаторам за багрепорты!
Это вам так только кажется. :-) Из всей кафедры я один слышал про R, но не использовал, а обычно используется Excel. Ну, это, наверное, действительно от кафедры зависит. У нас все поголовно рутом пользуются, а уж чтобы Excel'ем данные обрабатывать - такого я ещё не видел ;)
Спасибо уважаемым комментаторам за багрепорты! ;) Ваши посты всегда очень интересные, даже с багами.
@lizardie пишет...
Ну, это, наверное, действительно от кафедры зависит.
На кафедре прикладной математики кто-то слышал про Linux, а кое-кто даже про латех. У нас на кафедре латех знают трое. Технический университет, я напоминаю...
У нас все поголовно рутом пользуются, а уж чтобы Excel'ем данные обрабатывать - такого я ещё не видел ;)
Вы ещё не видели, как тут отчёты оформляют. Людям со слабой психикой такое лучше не видеть, не то, что участвовать.
Ваши посты всегда очень интересные, даже с багами.
Спасибо :-)
А то мне после некоторых постов будто слышится "три тысячи чертей! рваные аккордеоны! повесить этого баяниста на форс-марса-рее!" и что-то дальше неразборчиво :-))
set key width -7
-ещё красивее :)
Спасибо большое за данную статью!! Желаю вам успехов!Любую вашу статью читаю с большим интересом!!
Спасибо за ваши статьи по Гнуплоту. Сам только недавно (с полгода назад) перешёл на него, хотя впервые виндовый гнуплот использовал ещё на 1-ом курсе. У нас все поголовно пользуются Графером, причём почему-то особенно фанатеют по 5-ой версии этой программы. Ещё строят графики в Delphi и даже это считается на кафедре хорошим стилем для быстрого построения. Алгоритмы, естественно, тоже на Delphi писаны.
в описании директивы every не упомянут важный момент:
строки и блоки данных нумеруются, начиная с нуля, не с единицы.
и, кстати, что такое эти "блоки"?
Необходимо на ось х нанести три даты отбора проб произведенные с различным интервалом как это сделать?
("16.04" 1, "27.05" 2, "14.06" 3) - не получается При указании месяцев тоже самое. Подпись оси х исчезает вообще и в первом и во втором случае.
Михаил, у меня вопрос к Вам, как к специалисту :)
Не знаете ли Вы хорошего способа аппроксимировать в Octave полученные экспериментально данные? Набор из polyfit/polyval дает хорошее приближение лишь на небольшом участке данных.
@Ёлыч комментирует...
Михаил, у меня вопрос к Вам, как к специалисту :)
А почему со смайликом? Ну я не профессор, конечно, но до некоторой степени разбираюсь в предмете.
Не знаете ли Вы хорошего способа аппроксимировать в Octave полученные экспериментально данные?
Ёлыч, it depends. Из того, что я знаю: Least Squares, Weighted Lest Squares, Robust least squares, Non-linear approximation (Trusted region, Newton method). Это есть в Матлабе. Про Октаву не уверен, но в Октаве3 есть уже почти всё. Хотя сообщения об ошибках там всё такие же укуренные...
Набор из polyfit/polyval дает хорошее приближение лишь на небольшом участке данных.
Я не знаю, что стоит за этой фукнцией. А если я правильно помню, то это аппроксимация полиномами по Minimul least squares (то есть даже не weighted).
Так как я не телепат, а данных нет, могу дать ссылку. Это черновики матлабовских кодов для создания HDR из нескольких массивов данных. Там я использовал Trusted Region. По ссылке вообще можно накопать много познавательного (это архив моих матлабовских поделок :-)). Код местами абсолютно дубовый, но рабочий - это я для своего проекта по HDR делал.
Михаил, сразу хочу сказать спасибо, поскольку уже есть от чего оттолкнуться. Ну а теперь, по-порядку...
На счет смайлика - ирония была лишь по поводу самого вопроса. Ни малейшей попытки бросить тень на Вашу осведомленность не было.
На счет polyfit/polyval - Вы правы, с помощью этих функций реализуется лишь аппроксимация полиномами (метод наименьших квадратов). Я пытался найти что-нибудь по нелинейной аппроксимации, но мои попытки не увенчались успехом.
Ну и, конечно же, стоило показать исходные данные. Исправляюсь. По ссылке можно посмотреть на то, как выглядит простой plot() для одного из рядов данных.
Проблема в том, что вся эта "расческа" - результат ошибки, сильно зависящей от величины параметров. В результате, если попытаться построить не двумерный график, а поверхность по двум параметрам, то получается нечто совершенно неразборчивое.
@Ёлыч комментирует...
На счет смайлика - ирония была лишь по поводу самого вопроса.
Вопросы мне можно задавать запросто. Вплоть до калибра "есть ли жизнь на Марсе". Не факт, что я на них отвечу, конечно :-)
На счет polyfit/polyval - Вы правы, с помощью этих функций реализуется лишь аппроксимация полиномами (метод наименьших квадратов).
Точно. Но minimum least squares нам тут точно не поможет. Вот что бы я сделал, так это для начала сгладил бы данные, скажем, медианным фильтром - он эти выбросы хорошо должен убрать. Но я не знаю специфики задачи, и, кроме того, на осях отложены неизвестные величины (оси не подписаны).
Я пытался найти что-нибудь по нелинейной аппроксимации, но мои попытки не увенчались успехом.
Не думаю, что это поможет в данном случае. Если посмотреть на тот код, который я привёл по ссылке, то он аппроксимирует прямой данные, которые очень близки к линейным. Но даже там были проблемы (в начале данных и в конце есть нелинейности, и Trusted region был использован для того, чтобы они не влияли на результат аппроксимации).
В данном случае данные надо сначала сгладить, чтобы облегчить задачу при подгонке. Я бы серьёзно посмотрел в сторону Weighted Lest Squares - вес в данном случае хорошо бы сделать обратным расстоянию от среднего ($w_i = 1/\sigma$, где сигма - это standard deviation).
Ну и, конечно же, стоило показать исходные данные.
Было бы ещё круче, если бы на данных были подписи. Но и так сойдёт.
В результате, если попытаться построить не двумерный график, а поверхность по двум параметрам, то получается нечто совершенно неразборчивое.
Аппроксимацией поверхностей я не занимался (хотя может и придётся), но это в общем та же песня, что и в одномерном случае. Пока я склоняюсь к weighted least squares.
Автор, вы великолепны.
С вашей помощью и помощью официальных манов осваиваю gnuplot.
Большой привет с химфака.
@Анонимный комментирует...
Автор, вы великолепны.
Ну так! Красив, как бог, и голова как дом Советов :-)
С вашей помощью и помощью официальных манов осваиваю gnuplot.
Серьёзно, оно того стоит. Графики на выходе получаются очень красивые. Кстати, написанные посты по Гнуплоту иногда обновляются, так что stay tuned.
Ну и традиционно, рад что помогает кому-то, кроме меня.
Отправить комментарий
Подписаться на RSS-ленту комментариев к этому посту.